GRAPHS IN DSA
What are Graphs?
Graph is a non-empty set of Nodes and Edges. Nodes are also called vertices (singular: vertex) and edges are also known as Arcs. In other words, graph is a collection of vertices and edges that connect two vertices. Graphs are more powerful data structure and have more applications the other data structures.Mathematically, a graph G is defined as the order pair of sets (V , E) where V is a set of vertices and E is a set of edges. Each edge is a pair (u , c) that represent a connection between u and c.
Types of Graphs:
There are many different types of graphs such as directed graphs, undirected graphs, weighted graphs and many more. Each of these graphs has its own uses and applications according to their specific properties and characteristics.
Uses / Applications of Graphs:
Graphs can be used to design ay world situations, such as social networking (i.e., Friends of friend, mutual friends on Facebook), Computer networks, road networks (i.e., Google maps: Road or path between two or more cities, etc.), and many more.They ae used in various algorithms and data structure, such as shortest path algorithms and minimum spanning tree algorithms. Details are given below:
Social networks: Social media platforms like Facebook and LinkedIn use graphs to model relationships
between users. Each user is a node in the graph, and edges represent friendships or connections between
users.
Routing algorithms: Graphs are used in routing algorithms for finding the shortest path between two
points in a network. For example, the Google Maps application uses a graph to represent the road
network, with nodes representing intersections and edges representing roads.
Computer networks: Graphs are used to model computer networks, with nodes representing devices and
edges representing connections between devices. Network analysis can be done using graphs to identify
bottlenecks and optimize performance.
Recommendation systems: Many recommendation systems use graphs to represent similarities between
items. For example, a music recommendation system may represent songs as nodes and edges represent
how similar songs are to each other.
Biology: Graphs are used to model protein interactions, gene regulatory networks, and metabolic
pathways in biology. These models help researchers understand the complex interactions between
biological molecules.
Image processing: Graphs are used in image processing to represent the relationships between pixels. For
example, graphs can be used to detect edges in an image by identifying groups of pixels with high
connectivity.
Basic Terminologies of Graphs:
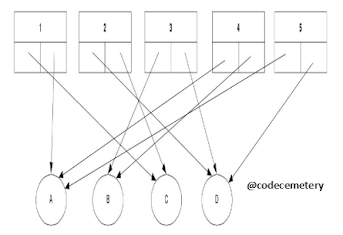
- Vertex (or Node): A vertex is a point in a graph. It can represent an object or entity in the real world or an abstract concept. Vertices are often represented as circles in a graph diagram.
- Edge: An edge is a line connecting two vertices in a graph. It represents a relationship or connection between the two vertices. Edges can be directed or undirected.
- Adjacent Nodes: Two nodes are said to be adjacent of there's an edge present between them.
- Directed Graphs: In a directed graph, edges have a direction or an arrow indicating the flow of the relationship.
- Undirected Graphs: In an undirected graph, edges do not have a direction and can be traversed in both directions.
- Weight: Numeric value associated with the node and/or edge.
- Weighted Graphs: In a weighted graph, each edge is assigned a weight or a cost. Weighted graphs are used to represent real-world problems where edges have different costs or values. weights can be written over vertices or edges or both. if one node is weighted other nodes must be weighted or if one edge is weighted then all other edges must be weighted. (Given graph has weights along with the both nodes and edges)
- Path: A path is a sequence of edges that connects a sequence of vertices in a graph. The length of a path is the sum of the weights of the edges in the path.
- Connected Graphs: A graph is said to be connected if there is a path between any two vertices in the graph.
- Disconnected Graphs: In a disconnected graph, there are one or more pairs of vertices that are not connected by a path.
- Cycle: A cycle is a path that starts and ends at the same vertex. Cycles can be of different lengths and can be used to represent repetitive behavior or loops in a system.
- Cyclic Graphs: A graph is said to be cyclic if it contains at least a cycle in it.
- Acyclic Graphs: A graph is Acyclic if it doesn't contain any cycle in it.
- Connected Graphs: A graph is said to be connected if there is a path between any two vertices in the graph.
- Disconnected Graphs: In a disconnected graph, there are one or more pairs of vertices that are not connected by a path.
- Complete Graphs: In a complete graph, each vertex is connected to every other vertex by an edge. Complete graphs are used to model problems where every pair of vertices has a relationship or connection.
Representation of graphs:
There are following some ways to represent a graphs:
Adjacency Matrix:
An adjacency matrix is a two-dimensional array where the rows and columns represent vertices in a graph,
and each entry represents an edge between two vertices. If the entry is 1, it means there is an edge
between the corresponding vertices, and if it's 0, there is no edge. For an undirected graph, the matrix is
symmetric along the diagonal. This representation is good for dense graphs, where most vertices are
connected to each other. See figure:
Adjacency List:
An adjacency list is a list of lists where each vertex has a list of its adjacent vertices. This representation is
good for sparse graphs, where few vertices are connected to each other. It is also more memory efficient
than an adjacency matrix for such graphs. See figure:
An edge list is a list of edges, where each edge is represented as a pair of vertices. This representation is simple and compact, but it doesn't provide any immediate information about which vertices are connected to which others.











0 Comments